Monte Carlo methods for option pricing
In mathematical finance, a Monte Carlo option model uses Monte Carlo methods to calculate the value of an option with multiple sources of uncertainty or with complicated features.[1]
The term 'Monte Carlo method' was coined by Stanislaw Ulam in the 1940s. The first application to option pricing was by Phelim Boyle in 1977 (for European options). In 1996, M. Broadie and P. Glasserman showed how to price Asian options by Monte Carlo. In 2001 F. A. Longstaff and E. S. Schwartz developed a practical Monte Carlo method for pricing American-style options.
Contents |
Methodology
In terms of theory, Monte Carlo valuation relies on risk neutral valuation.[1] Here the price of the option is its discounted expected value; see risk neutrality and Rational pricing: Risk Neutral Valuation. The technique applied then, is (1) to generate several thousand possible (but random) price paths for the underlying (or underlyings) via simulation, and (2) to then calculate the associated exercise value (i.e. "payoff") of the option for each path. (3) These payoffs are then averaged and (4) discounted to today. This result is the value of the option.[2]
This approach, although relatively straightforward, allows for increasing complexity:
- An option on equity may be modelled with one source of uncertainty: the price of the underlying stock in question.[2] Here the price of the underlying instrument
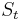is usually modelled such that it follows a geometric Brownian motion with constant drift 
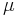and volatility 
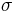. So: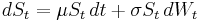 
, where 
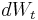is found via a random sampling from a normal distribution; see further under Black–Scholes. (Since the underlying random process is the same, for enough price paths, the value of a european option here should be the same as under Black Scholes).
- In other cases, the source of uncertainty may be at a remove. For example, for bond options [3] the underlying is a bond, but the source of uncertainty is the annualized interest rate (i.e. the short rate). Here, for each randomly generated yield curve we observe a different resultant bond price on the option's exercise date; this bond price is then the input for the determination of the option's payoff. The same approach is used in valuing swaptions,[4] where the value of the underlying swap is also a function of the evolving interest rate. (Whereas these options are more commonly valued using lattice based models, for path dependent interest rate derivatives - such as CMOs - simulation is the primary technique employed.[5]) For the models used to simulate the interest-rate see further under Short-rate model; note also that "to create realistic interest rate simulations" Multi-factor short-rate models are sometimes employed.[6]
- Monte Carlo Methods allow for a compounding in the uncertainty.[7] For example, where the underlying is denominated in a foreign currency, an additional source of uncertainty will be the exchange rate: the underlying price and the exchange rate must be separately simulated and then combined to determine the value of the underlying in the local currency. In all such models, correlation between the underlying sources of risk is also incorporated; see Cholesky decomposition: Monte Carlo simulation. Further complications, such as the impact of commodity prices or inflation on the underlying, can also be introduced. Since simulation can accommodate complex problems of this sort, it is often used in analysing real options [1] where management's decision at any point is a function of multiple underlying variables.
- Simulation can similarly be used to value options where the payoff depends on the value of multiple underlying assets [8] such as a Basket option or Rainbow option. Here, correlation between assets is likewise incorporated.
- As required, Monte Carlo simulation can be used with any type of probability distribution, including changing distributions: the modeller is not limited to normal or lognormal returns;[9] see for example Datar-Mathews Method for Real Option Valuation. Additionally, the stochastic process of the underlying(s) may be specified so as to exhibit jumps or mean reversion or both; this feature makes simulation the primary valuation method applicable to energy derivatives.[10] Further, some models even allow for (randomly) varying statistical (and other) parameters of the sources of uncertainty. For example, in models incorporating stochastic volatility, the volatility of the underlying changes with time; see Heston model.
Application
As can be seen, Monte Carlo Methods are particularly useful in the valuation of options with multiple sources of uncertainty or with complicated features, which would make them difficult to value through a straightforward Black–Scholes-style or lattice based computation. The technique is thus widely used in valuing path dependent structures like lookback- and Asian options [9] and in real options analysis.[1][7] Additionally, as above, the modeller is not limited as to the probability distribution assumed.[9]
Conversely, however, if an analytical technique for valuing the option exists—or even a numeric technique, such as a (modified) pricing tree [9]—Monte Carlo methods will usually be too slow to be competitive. They are, in a sense, a method of last resort;[9] see further under Monte Carlo methods in finance. With faster computing capability this computational constraint is less of a concern.
References
Notes
- ^ a b c d Marco Dias: Real Options with Monte Carlo Simulation
- ^ a b Don Chance: Teaching Note 96-03: Monte Carlo Simulation
- ^ Peter Carr and Guang Yang: Simulating American Bond Options in an HJM Framework
- ^ Carlos Blanco, Josh Gray and Marc Hazzard: Alternative Valuation Methods for Swaptions: The Devil is in the Details
- ^ Frank J. Fabozzi: Valuation of fixed income securities and derivatives, pg. 138
- ^ Donald R. van Deventer (Kamakura Corporation): Pitfalls in Asset and Liability Management: One Factor Term Structure Models
- ^ a b Gonzalo Cortazar, Miguel Gravet and Jorge Urzua: The valuation of multidimensional American real options using the LSM simulation method
- ^ global-derivatives.com: Basket Options - Simulation
- ^ a b c d e Rich Tanenbaum: Battle of the Pricing Models: Trees vs Monte Carlo
- ^ Les Clewlow, Chris Strickland and Vince Kaminski: Extending mean-reversion jump diffusion
Articles
- Boyle, Phelim P., Options: A Monte Carlo Approach. Journal of Financial Economics 4, (1977) 323-338
- Broadie, M. and P. Glasserman, Estimating Security Price Derivatives Using Simulation, Management Science, 42, (1996) 269-285.
- Longstaff F.A. and E.S. Schwartz, Valuing American options by simulation: a simple least squares approach, Review of Financial Studies 14 (2001), 113-148
Resources
Books
- Bruno Dupire (1998). Monte Carlo:methodologies and applications for pricing and risk management. Risk.
- Paul Glasserman (2003). Monte Carlo methods in financial engineering. Springer-Verlag. ISBN 0-387-00451-3.
- Peter Jäckel (2002). Monte Carlo methods in finance. John Wiley and Sons. ISBN 0-471-49741-X.
- Don L. McLeish (2005). Monte Carlo Simulation & Finance. ISBN 0-471-67778-7.
- Christian P. Robert, George Casella (2004). Monte Carlo Statistical Methods. ISBN 0-387-21239-6.
Software
- Fairmat (freeware) modeling and pricing complex options
- MG Soft (freeware) valuation and Greeks of vanilla and exotic options
External links
- Monte Carlo Simulation, Prof. Don M. Chance, Louisiana State University
- Pricing complex options using a simple Monte Carlo Simulation, Peter Fink (reprint at quantnotes.com)
- MonteCarlo Simulation in Finance, global-derivatives.com
- Monte Carlo Derivative valuation, contd., Timothy L. Krehbiel, Oklahoma State University–Stillwater
- Applications of Monte Carlo Methods in Finance: Option Pricing, Y. Lai and J. Spanier, Claremont Graduate University
- Option pricing by simulation, Bernt Arne Ødegaard, Norwegian School of Management
- Monte Carlo Method, riskglossary.com
|
|||||||||||||||||||||||||||||||||||||